قانون مساحة متوازي الاضلاع

إذا كان ارتفاع متوازي الأضلاع غير معروف فيمكن استخدام علم المثلثات للعثور على المساحة حيث تصبح المساحة ab sin x حيث a و b هما طولا ضلعين متلاقيين في المتوازي و x هي الزاوية المحصورة بين الضلعين.

قانون مساحة متوازي الاضلاع. قانون مساحة متوازي الاضلاع. الارتفاع 96 6 16 سم. قانون محيط المثلث ومساحته. قانون مساحة متوازي الاضلاع.

قانون مساحة متوازي الاضلاع متوازي الأضلاع أحد الأشكال الهندسة المميزة الذي دراستها في مجال الهندسة والمعمار يتميز متوازي الأضلاع أن لديه 4 أضلاع كل ضلعين متساويين ومتوازيين سوف نتعرف عبر موقع زيادة من خلال مقالنا عن قانون المساحة الخاصة متوازي الأضلاع وكل المعلومات. مساحة متوازي الاضلاع طول القاعدة الارتفاع المناظر لها. ما هو قانون مساحة المثلث. قانون مساحة المثلث قائم الزاوية.

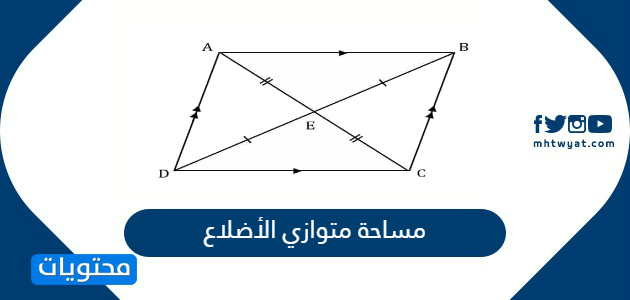
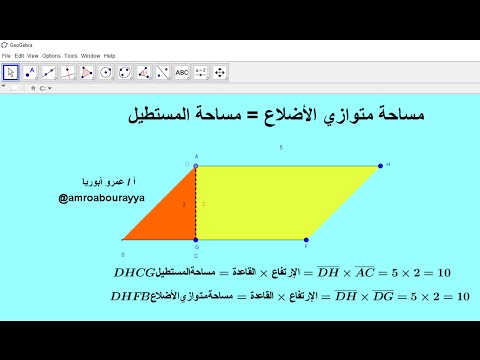
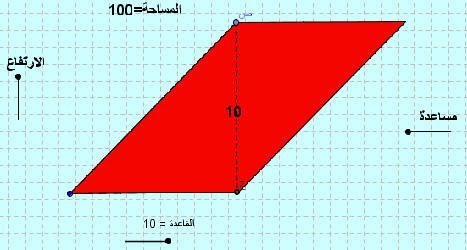
إن مساحة متوازي الأضلاع م تساوي طول القاعدة ل مضروبا بالمسافة العامودي ة بين القاعدتين ع ويمكن تمثيلها بالر موز الر ياضي ة على الشكل م ع ل كما أن هناك العديد من القوانين الخاص ة ببعض حالات متوازي الأضلاع دون بعضها الآخر ومنها ما يأتي. إن تحقق واحد من الخصائص السابقة في مضلع رباعي محدب يعني أن الشكل متوازي أضلاع كما أن إثبات أن ضلعين متقابلين متوازيين ومتقايسيين في آن. مجموع مربعات أطوال الأضلاع تساوي مجموع مربعي طولي القطرين هذا هو قانون متوازي الأضلاع. قانون مساحة متوازي الاضلاع بدون الارتفاع.

قانون مساحة المثلث متساوي الأضلاع. قانون محيط المثلث متساوي الساقين. مجموع كل زاويتين متحالفتين على ضلع واحد 180. مساحة متوازي الاضلاع 8 12 96 سم2.

6 س س 1 ومنه 6 س س وبحل هذه المعادلة وإيجاد قيمة س عن طريق تحليلها إلى س 2 س 3 6 فإن قيم س تساوي س 2 وس 3 وباستبعاد القيمة السالبة ينتج أن طول القاعدة 2سم أما الارتفاع فيساوي س 1 2 1 3سم. قانون مساحة متوازي الأضلاع عبر موقع محتوى متوازي الأضلاع بالإنجليزية يعني parallelogram وهو شكل هندسي له أربعة أضلاع يمكن اعتباره مستطيل أو مربع أو معين إذا حقق بعض الشروط التي سوف نذكرها لاحقا فتعالوا نتعرف عبر موقع محتوى على خصائصه وقانون حساب. الارتفاع المناظر للضلع الاصغر الارتفاع الاكبر المساحة القاعدة الصغرى. مواضيع ذات صلة بـ.